A Quandary: A Lost Cities Endgame Decision

Recently I have been limited to gaming done online due to time constraints. The current source is a turn based site in which players can log in periodically and make a move, slowly making progress in many games. Playing games in this manner isn't an ideal, but it does provide the additional time to deliberate over some interesting situations in some of my favorite games.

I came across a tough decision in one such game that I wanted to do a write up on as I have had difficulty finding the optimal decision. I've included a quick synopsis of game play but if you are already comfortable feel free to skip the overview.

I present to you my most recent quandary:

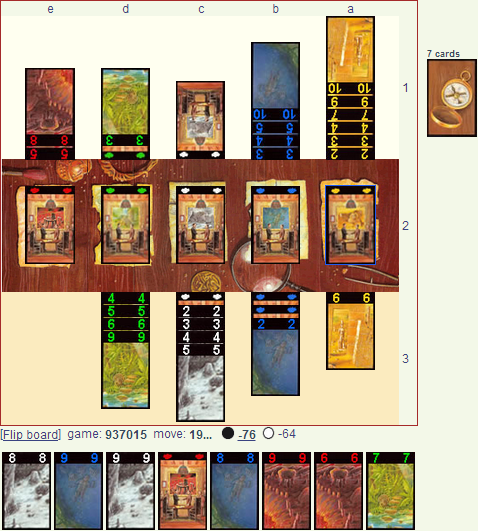You have -76 pts, 7 cards remain, what should you do this turn?

Lost Cities Overview

In Lost Cities you are attempting to place cards in ascending order using investment cards to start an expedition that function as multipliers to generate higher scores. Each color you place a card in scores (Sum of card values minus 20 points) [multiplied by] investment cards. Additionally a bonus of 20 points can be added for playing eight or more cards in a color.

The Quandary

First let me lay out the cards we should be focused on, first lets look at the cards we currently have and find our current maximum possible score.

Currently we can play the Blue 8 & 9 for 51 points (8 + 9 * 3) and the White 8 & 9 for 34 points (8 + 9 * 2). Adding these totals to our current -76 points we find our current maximum score is 9 points. This is assuming we don't draw any of the cards we need along the way (see below).

Our opponent currently is sitting at -64 points and we can only speculate as to their holdings. There are six remaining cards that can help them, the White 6, 7 & 10, the Green 8 & 10 (We hold the Green 7) and the Red 10 (We hold the Red 9). The total of these cards is worth 92 points and when added to their current score they reach a maximum score of 28 points.

With 7 cards remaining we can play and draw from the deck twice, followed by drawing from the discard piles if we hit one of the additional cards we are looking for. This allows us to play a maximum of five cards before the game ends. We need the White 6, 7 or 10, or the Blue 6 or 7. The Yellow 8 is also a card we can use but we would pick it last for our dodge ball team on the playground.

As you can see our opponent may literally hold the upper hand. They can play from four to six cards depending on their pace of the game dependent on what cards they have remaining.

So where is the dilemma?

Do we play the Blue 8 (Hoping to draw the White 6, 7 or 10)
Or do we play the White 8 (Hoping to draw the Blue 6 or 7)

Weighing the Options

By playing the White 8 we hope to draw the Blue 6 which would be worth 18 points (bringing us to 27) or the Blue 7 which would be worth 21 points (bringing us to 30).

By playing the Blue 8 we hope to draw the White 6, 7 or 10, not only scoring us 12, 14 or 20 points respectively but also (if you noticed) bringing us to 8 cards in White and earning us a smooth +20 points. The worst of these cards nets us +32 points and brings us above our opponent's theoretical max score, so we can ignore marginal benefits and treat all three cards equally.

So you may be saying "This is simple, the three white cards are game winners, so Play the Blue 8 as there are only two blue cards that benefit us and one of those doesn't necessarily always win us the game.

You'd be correct. If this was in a vacuum. But we don't play board games in a vacuum. That would be strange and unnecessarily difficult. Lets roll out the context.

The Context (You thought you were done, didn't you?)

This game is currently in turn 19. A turn by this definition consists of each player taking a turn (So in baseball terms we are in the bottom of the 19th inning).

On turns 1 & 2 they played the Green Investment & Green 3.

On turn 3 they played the White Investment (I played the White 5 on turn 15).

On turn 8 they completed their blue expedition by playing the Blue 10 (I'll explain why this is important in a moment).

Inductive Reasoning

Given the above information we can assert several premises. This is against an experienced player so the following observations will usually hold true at this (late) point in the game.

• Players like to play the next sequential card so as to maximize their future outcome.
• Players likes to play an investment with an additional card of that color in hand for assurance.
• Players will hold useless cards until they can be safely discarded as to not benefit opponents.

In this case we could guess they would only play the White Investment card if they held another white card in their hand on turn 3. They would also have played a White 6 by now if they had it. They may or may not have played a White 7 by now if they had it but certainly not the White 10 (As they would forfeit the potential White 6, 7, 8 & 9 scoring possibilities).

Our opponent has no knowledge that we hold the Green 7, so they may elect to hold the Green 8 or 10 for now.

They have no use for any more Blue cards as they played their Blue 10 on turn 8, this does mean they have had 11 turns to accrue additional blue cards. We have no way to tell as they would retain these cards.

Conclusion

So should you play the White 8 or the Blue 8 or more importantly, does it actually make a difference in the outcome? I'll revisit this next time with several approaches in order to help identify the potential optimal decision.