A Quick Probability Conundrum: Follow-up

Last week, I posed the question "if I have twelve cards numbered 1-12, draw three per day without replacement, record their numbers, and then replace them and shuffle, how many days will it take before I should expect to see all twelve?" I was interested in seeing either a simulated or analytical result, and I got convincing ones of each.

Analytical solution

My friend Angelo is an astrophysics/applied math double major, so it's pretty safe to say he's better at math than I am. Here's his analytical solution to the problem, slightly limited by the "three cards per day" restriction.

P(x) = (# of strings of length x that contain each digit between 1 and 12 at least once) / (number of total possible strings of length x)

 = 1 - ((# of strings missing 1 or more digit) / (12^x))

Actually, as he points out, this yields the number of cards you'd need to look at, not the number of days--but that's easy enough to fix by dividing by three. Here's the plot of the analytical cdf:

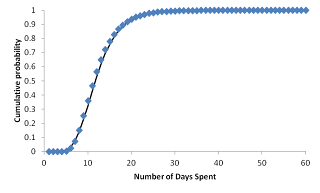
which appears to cross P(x) = 0.5 around card number 35, or roughly 11 or 12 days. Here's his analytical pdf along with a simulation (n = 10000):

They're a little off, and the simulation isn't quite smooth at n = 10000, but the agreement is reasonably good. For the "magic number" of P = 0.5, Angelo's analytical solution gives 11.7 days, and the simulated solution gives 12.7. Here's his full write-up.

More simulations

I did a simulation of my own with the following logic: start with an array of twelve zeros, pick three of those zeros at random to become ones, and repeat the process until all the zeros are ones. Then do the whole thing over again, 50000 times. My simulation was done in MATLAB. Here's the distributions I came up with:

I get basically the same shape as Angelo's graphs, though the extra 40000 simulations helps make the pdf a lot smoother. It's most likely to take 11 or 12 days, and the mean value of the pdf is 12.7, just like with Angelo's simulation. Strangely, my cdf crosses P(x) = 0.5 at x = 11.7 days, exactly one day too soon, so it's likely I messed up the integration of the pdf.


I got a nice verification of my simulation from another friend, Forrest, who actually does numerical simulations for a living, so there's a good chance his is far more rigorous than mine. I don't have his simulation code, but after one million simulations, his cdf looks similar enough to mine (note the change in scale on the x-axis):

Forrest concludes that the "magic number" is somewhere between 11 or 12, putting his best estimate at 11.3.

Conclusion

The analytical solution and all three simulations put the P = 0.5 threshold somewhere between 11 and 13 days, and the mode or most likely occurrence of both pdfs is essentially a tossup between days 11 and 12. If we're looking for a single numerical answer to the question, I'm putting it at day 12: you're most likely to have seen all twelve cards on day 12. (Follow-up question: is it a coincidence that the number of the "critical" day is also the number of cards in the stack?)

Other interesting facts: it is in fact possible to be done on day 4, but it appears to be exceedingly rare. Only once in 50000 trials (or 0.002% of the time) did my simulation see all twelve cards in only four days. It's equally rare to have to spend more than 50 days: one simulation in 50000 (again, 0.002%) took 57 days to complete, but no other simulations took longer than 48 days.

Thanks to everyone who helped solve this problem! I'm both pleased and amazed that I found such an abstract, academic problem that is nevertheless relevant to real-world game design.